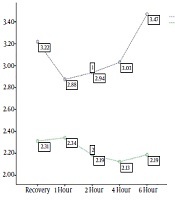
International Journal of Cancer Management The Official Journal of Cancer Research Center (CRC), Shahid Beheshti University of Medical Sciences
.png)
OVERVIEW
Organization: Cancer Research Center (CRC), Shahid Beheshti University of Medical Sciences
ISSN: e: 2538-497X | p: 2538-4422
Frequency: Monthly


.png)